351. Android Unlock Patterns

Given an Android 3x3 key lock screen and two integers m and n, where 1 ≤ m ≤ n ≤ 9, count the total number of unlock patterns of the Android lock screen, which consist of minimum of m keys and maximum n keys.

Rules for a valid pattern:

1. Each pattern must connect at least m keys and at most n keys.
2. All the keys must be distinct.
3. If the line connecting two consecutive keys in the pattern passes through any other keys, the other keys must have previously selected in the pattern. No jumps through non selected key is allowed.
4. The order of keys used matters.

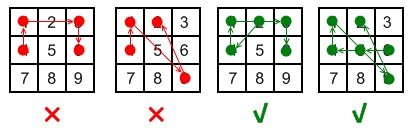
Explanation:

| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |

Invalid move: 4 - 1 - 3 - 6 
Line 1 - 3 passes through key 2 which had not been selected in the pattern.

Invalid move: 4 - 1 - 9 - 2
Line 1 - 9 passes through key 5 which had not been selected in the pattern.

Valid move: 2 - 4 - 1 - 3 - 6
Line 1 - 3 is valid because it passes through key 2, which had been selected in the pattern

Valid move: 6 - 5 - 4 - 1 - 9 - 2
Line 1 - 9 is valid because it passes through key 5, which had been selected in the pattern.

Example:
Given m = 1, n = 1, return 9.

Solution:

Intuitively, we could use DFS backtracking to solve this problem.

The difficulty is that at a current state, how do we check which number we can go next?

We create a skip array to handle this.

skip[i][j] denotes if we go from i to j, which number we cannot skip.

In other words, if we skip this number, the output will be invalid.

Now we deal with the DFS.

We find 1, 3, 7, 9 are symmetric. 2, 4, 6, 8 are also symmetric.

This means that if we know the total number of valid patterns start from 1, we know the numbers start from 3, 7, and 9.

If we know the total number of valid patterns start from 2, we know the numbers start from 4, 6, and 8.



Code:

public class Solution {
    
    public final int[][] skip = new int[10][10];
    
    public int numberOfPatterns(int m, int n) {
        skip[1][3] = skip[3][1] = 2;
        skip[1][7] = skip[7][1] = 4;
        skip[3][9] = skip[9][3] = 6;
        skip[7][9] = skip[9][7] = 8;
        skip[1][9] = skip[9][1] = skip[3][7] = skip[7][3] = 5;
        skip[2][8] = skip[8][2] = skip[4][6] = skip[6][4] = 5;
        
        int result = 0;
        boolean[] visited = new boolean[10];
        for (int i = m; i <= n; i++) {
            result += dfs(1, visited, i - 1) * 4;
            result += dfs(2, visited, i - 1) * 4;
            result += dfs(5, visited, i - 1);
        }
        return result;
    }
    public int dfs(int curr, boolean[] visited, int remain) {
        if (remain == 0) {
            return 1;
        }
        int result = 0;
        visited[curr] = true;
        for (int next = 1; next <= 9; next++) {
            int jump = skip[curr][next];
            if (!visited[next] && (jump == 0 || visited[jump])) {
                result += dfs(next, visited, remain - 1);
            }
        }
        visited[curr] = false;
        return result;
    }
}